Maximum Sum Rectangle in a 2D array

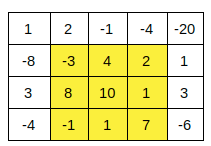
         Sample Test case:

                    


        Answer
                                               

      Naive Approach:

        The naive approach to find the maximum sum rectangle in a 2D array involves generating all possible submatrices and calculating their sum, and then selecting the maximum sum submatrix among them.  Each submatrix is generated by selecting its top-left corner and bottom-right corner. 

        Although this approach is simple to implement, it is not efficient for large inputs since its time complexity is very high. Therefore, more efficient algorithms like Kadane's algorithm for 2D arrays are used to solve this problem.


Code: (C++)
        
#include <iostream>
#include <bits/stdc++.h>
using namespace std;

int maxSumRectangle(vector<vector<int>>& arr, int n, int m)
{
int nrow = arr.size();
int ncol = arr[0].size();

int maxSum = INT_MIN;

for (int i = 0; i < nrow; i++)
{
for (int j = 0; j < ncol; j++)
{
int topLeft = arr[i][j];


for (int k = i; k < nrow; k++)
{
for (int l = j; l < ncol; l++)
{
int topRight = arr[k][l];
int tempSum = 0;

for (int row = i; row <= k ; row++)
{
for (int col = j; col <= l; col++)
{
tempSum += arr[row][col];
}
}

if (tempSum > maxSum)
{
maxSum = tempSum;
}
}
}

}
}
return maxSum;

}



int main()
{

vector<vector<int>> arr = {{-2, 1, -3, 4},
{5, -6, 7, -8},
{9, -10, 11, -12}};

int n = arr.size();
int m = arr[0].size();

cout << maxSumRectangle(arr, n, m) << endl;
return 0;
}



            
Optimized Code using Kadane's
    
    Here  the left and right pointers define the left and right boundaries of the current sub-rectangle. The running_row_sum array keeps track of the sum of each row in the sub-rectangle, where the sum of each row is calculated incrementally by adding the value of the new column to the previous row sum. Then, Kadane's algorithm is used to find the maximum subarray sum in the running_row_sum array, which corresponds to the maximum sum rectangle for the current sub-rectangle.

    Overall, the algorithm works by iteratively creating all possible sub-rectangles by varying the left and right columns, and for each sub-rectangle, it computes the sum of each row by adding values of new columns incrementally. Finally, it finds the maximum sum rectangle in the row sum array using Kadane's algorithm. The algorithm has a time complexity of O(N^3) for an NxN matrix.


Code : (C++)

#include <bits/stdc++.h>
using namespace std;

int kadane(vector<int> arr) {
int max_sum = INT_MIN;
int curr_sum = 0;
for (int num : arr) {
curr_sum = max(num, curr_sum + num);
max_sum = max(max_sum, curr_sum);
}
return max_sum;
}

int maxSumRectangle(vector<vector<int>> matrix, int rows, int cols) {
int max_sum = INT_MIN;
for (int left = 0; left < cols; left++) {
vector<int> running_row_sum(rows, 0);
for (int right = left; right < cols; right++) {
for (int i = 0; i < rows; i++) {
running_row_sum[i] += matrix[i][right];
}
max_sum = max(max_sum, kadane(running_row_sum));
}
}
return max_sum;
}

int main() {
vector<vector<int>> arr = {{1, 2, -1, -4, -20},
{-8, -3, 4, 2, 1},
{3, 8, 10, 1, 3},
{-4, -1, 1, 7, -6}};
int rows = arr.size();
int cols = arr[0].size();
cout << maxSumRectangle(arr, rows, cols) << endl;
return 0;
}

    

Comments

Post a Comment

Popular posts from this blog

Hackerrank - Quicksort 2 - Sorting

Image
     Problem Submissions Leaderboard Discussions In the previous challenge, you wrote a partition method to split an array into two sub-arrays, one containing smaller elements and one containing larger elements than a given number. This means you 'sorted' half the array with respect to the other half. Can you repeatedly use partition to sort an entire array? Guideline In Insertion Sort, you simply went through each element in order and inserted it into a sorted sub-array. In this challenge, you cannot focus on one element at a time, but instead must deal with whole sub-arrays, with a strategy known as "divide and conquer". When partition is called on an array, two parts of the array get 'sorted' with respect to each other. If partition is then called on each sub-array, the array will now be split into four parts. This process can be repeated until the sub-arrays are small. Notice that when partition is called on just one of the numbers, the
Read more

SPECIAL STRING ARRAY

  Consider a non-empty string array inarr and a string instr. Identify and print outarr, based on the below logic: • For the string instr, generate a list of special strings specialstringlist. o List of special strings A special string for a string stris generated by right shiftingthe characters by one position. Last character will be shifted as the first character The newly generated special string is used as str for generating the next special string in the list Repeat the generation until the original string stris reached. o List of special strings would contain the string str. • Starting from the leftmost element, for each element in inarr. o Add the element of inarr to outarr if it is a subsequence in specialstringlist § Subsequence: A subsequence of a string str in the possible set of characters formed from string starting from left to right • If none of the elements from inarr is a subsequence of specialstringlist print -1 Note:  Perform case-insensitive comparison Input Format
Read more

Code Goda 2022 - Special Numbers

Problem Statement - 1 Mr. Agoji given a shuffled string made by randomly shuffling a special string.  A string will be called special only if it is formed by joining some special words any number of times. Special words are mapping of numbers (0 <= number < 10) to their words, for example, mapping of '0' to 'zero', mapping of  '1' to 'one', and so on.  Mr. Agoji is asked to convert the shuffled string into smallest special number. A special number is a number formed using numbers (0 <= number < 10) without any leading zeroes.  Mr. Agoji being not so good with numbers and strings ask for your help. Input Format  The first line of the input T contains the number of test cases,  1 <= T <= 100 For each test case.  There will be a, s shuffled string, on a separate line   1 <= s.length <= 100000  Output Format  For each test case, on the new line print the special number and if all the numbers are zero print zero. Sample Input  ewtooetz
Read more